In this post, we will see how we can manipulate and even create signals in the frequency domain rather than in the time domain. This post builds on the previous post of creating and visualizing time domain signals in GNU Radio.
With the introductory groundwork to how the code structure looks like done in the earlier posts, we will start to tinker with it. What we want to do now is to add an intermediate block after our source block. This block should add another sinusoid to the signal (like adding a new signal) - in the frequency domain. This activity can be broken down into two sub-steps:
- Create a new GNU Radio Block
- In the GNU Radio Block created in the step above, receive the signal, convert it to the frequency domain, add another signal at some desired frequency and convert the signal back to time domain.
Creating a new GNU Radio Block:
Ad-hoc blocks can be directly written in Python Scripts. Here is a sample one generated by using the Embedded Python Block utility from GNU Radio Companion:
"""
Embedded Python Blocks:
"""
import cmath
import math
import numpy as np
from gnuradio import gr
class custom_source(gr.sync_block): # other base classes are basic_block, decim_block, interp_block
"""Embedded Python Block template"""
def __init__(self,
samp_rate = 32e3,
): # only default arguments here
gr.sync_block.__init__(
self,
name='Sample Block', # will show up in GRC
in_sig=[np.complex64],
out_sig=[np.complex64]
)
# if an attribute with the same name as a parameter is found,
# a callback is registered (properties work, too).
self.samp_rate = samp_rate
def work(self, input_items, output_items):
output_items[0][:] = input_items[0][:]
return len(output_items[0])
The work() method and a more general form of it called general_work() method are employed and it is in these methods that any signal processing occurs. In the example above, the block subclasses the sync block of GNU Radio (number of output samples equals the number of input samples). In the constructor, we first initialize the base class with its parameters and then do any other initialization. Note that the number of input and output ports is specified in the call to initialize the sync block in the form of an array. in_sig = [np.complex64] implies that there is one input port (one element in the list/array) and it takes data of complex data type (defined by numpy module).
The work() method is passed the input samples across all ports in the object list input_items, and we are required to write the processed values in the output_items. The method returns the number of samples consumed from the input_items in this run of the method. For some background, GNU Radio creates chunks or arrays of definite length out of the samples being generated and makes them flow across the graph. We can determine what is the length of data array we require for our block, but right now, we don't do it. With the code above right now, the block will just sit there and pass data from one end to the other without doing anything.
Add a signal in the frequency domain:
OK. Now, we have an incoming stream of time domain samples - coming in blocks of 4096 samples per block (it isn't always so, but let us assume for the purpose of this post). We know beforehand that inside these samples is a signal in time domain - a waveform at, say, 100Hz. Suppose, we now want to add another signal to it which has the frequency of, say 4000Hz. How do we do it? One simple way was to have another signal source of 4000Hz and pass the two signals through an adder. The superposition of signals would add them up. But just for kicks (and some higher purpose), we want to do it in the frequency domain and not use a block called adder.
Consider this statement: There is an incoming signal, which if expressed in the frequency domain would be a vertical line (or impulse) at 100Hz. Since we get 4096 samples in one array, all representing some time instant snapshots of this signal, if possible, we could find exactly 4096 frequency bins in which these samples are contained in the frequency domain - since time and frequency have a kind of one-to-one correspondence. The concept is more intricate - but here, let us assert that it works. To see that, modify the custom block code as:
class custom_source(gr.sync_block): # other base classes are basic_block, decim_block, interp_block
"""Embedded Python Block template"""
def __init__(self,
samp_rate = 32e3,
freq = 4e3,
amp = 0.5): # only default arguments here
gr.sync_block.__init__(
self,
name='Sample Block', # will show up in GRC
in_sig=[np.complex64],
out_sig=[np.complex64]
)
# if an attribute with the same name as a parameter is found,
# a callback is registered (properties work, too).
self.samp_rate = samp_rate
self.freq_to_add = freq
self.signal_amp = amp
def work(self, input_items, output_items):
input_in_fft = np.fft.fftshift(np.fft.fft(input_items[0][:], len(output_items[0][:])))
input_in_fft[(len(output_items[0][:])/2)+int(self.freq_to_add)] = (self.signal_amp)*len(output_items[0][:])*1.0
output_items[0][:] = np.fft.ifft(np.fft.ifftshift(input_in_fft), len(output_items[0]))
return len(output_items[0])
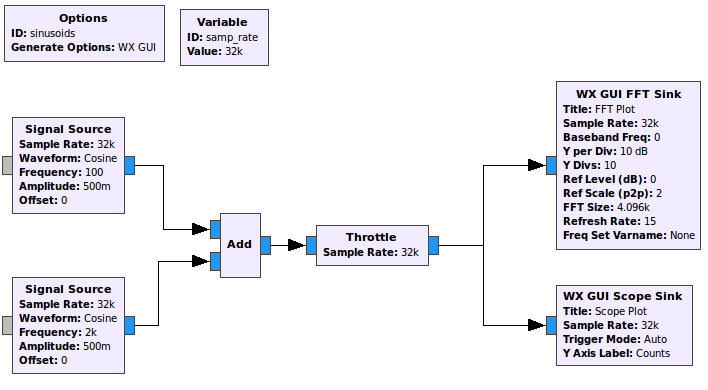
Modify the flowgraph connections as:
self.custom_block = custom_source(samp_rate, freq=2e3, amp=0.5)
##################################################
# Connections
##################################################
self.connect((self.analog_sig_source_x_0, 0), (self.custom_block, 0))
self.connect((self.custom_block, 0), (self.blocks_throttle_0, 0))
self.connect((self.blocks_throttle_0, 0), (self.wxgui_fftsink2_0, 0))
self.connect((self.blocks_throttle_0, 0), (self.wxgui_scopesink2_0, 0))
And run!
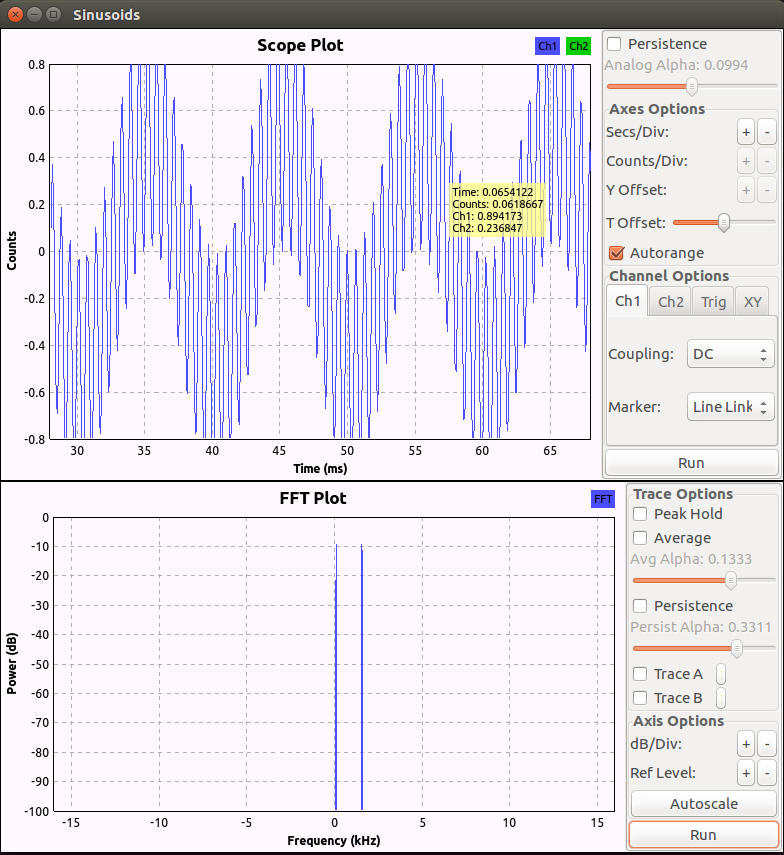
Observe that while there was just one frequency impulse in the previous post (generated by the signal source block), now the FFT plot shows two. The other one is due to the modification we did in our custom block. To appeal that we have infact done something which could very well be done in time domain too, contrast this with an addition in the time domain itself:

This was done with the following flowgraph:
So, by just adding one sample in the frequency domain with
input_in_fft[(len(output_items[0][:])/2)+int(self.freq_to_add)] = (self.signal_amp)*len(output_items[0][:])*1.0
we have effectively added a whole new signal!
OK, we cheated a bit there. The frequency added by mixing in the frequency domain is not what we wanted. We said that we wanted 2000Hz but the result isn't exact. In fact, it can be wildly different. This has to do with how FFT is computed. But, right now, the point being made is, we can do stuff in the time domain as well as the frequency domain! Maybe we should look into why this thing works, and what is so special about 4096 samples per block and our's choosing 4096 as the FFT size in our custom block. More on that later.
The source for this post can be viewed here.
